QUEMIN/ROYER/LORENZI
La suite de Fibonacci
Elle a été découverte par Fibonacci en 1202 et est une suite d'entiers dans laquelle chaque nombre est la somme des deux nombres qui le précèdent, on définit 1 et 0 (ou 1 et 1) comme les nombres initiaux. Il décrit cette suite dans son ouvrage "Liber abaci" où il décrit la croissance d'une population de lapins à l'aide de laquelle il démontre sa suite. Ceci pour expliquer le problème récréatif suivant : "Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ?".
Cependant pour que cette suite soit possible il faut que :
-il y ait un couple de lapin le premier mois
-les lapereaux ne procréent qu'au début du troisième mois
-chaque mois les couples pouvant procréer engendre un nouveau couple
-les lapins ne meurent jamais pour que la suite soit croissante
La suite peut donc s'expliquer par la formule suivante : où n est un entier naturel et où Fn définit le nombre de couple de lapins.
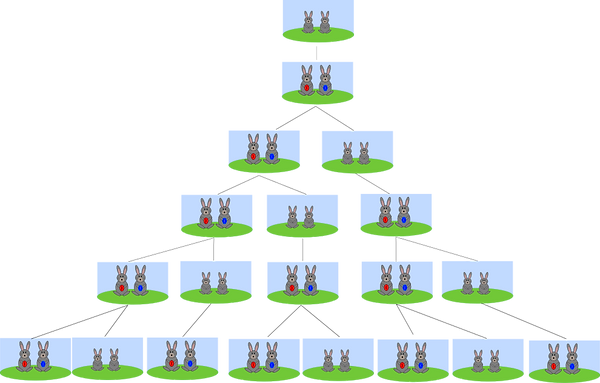
Le problème est illustré par le graphique suivant :