QUEMIN/ROYER/LORENZI
La spirale logarithmique

Spirale vient du grec ancien σπείρα / speira qui signifie enroulement. En mathématiques, le terme désigne en effet une courbe qui commence en un point centrale et s'en éloigne tout en tournant autour.
Une spirale qui se développe en trois dimensions est appelée hélice.
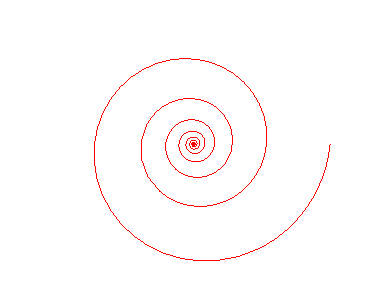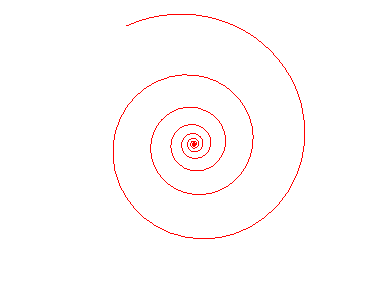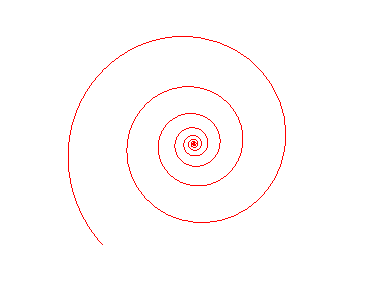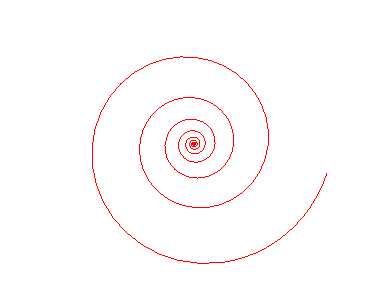
La spirale logarithmique possède en particulier possède des propriété spécifiques et très visuelles. Tout d'abord elle est connue pour son invariance qui a longtemps été la raison de son étude. C'est-à-dire que toutes rotations de la spirale revient à une homothéties (rétrécissement ou agrandissement) de même centre et de rapport e^-k.θ, elle revient donc à son identique pour
θ=0 mod2π.
Cela est vrai car il s'agit d'une spirale d'angle constant: l'angle entre sa tangente et son rayon est constant en tout point.
Plus simplement cela signifie que la spirale conserve la même forme en tournant sur elle-même. Comme vous pouvez le constater sur l'aniamtion ci-contre (tiré de mathcurve.com), à chaque fois que le figure s'agrandit d'un tour entier, elle se superpose avec l'ancienne version d'elle-même.
Son équation polaire est de la forme r=ab^θ ou a et b sont deux réels strictement positifs et b différent de 1(auquel cas la figure est un cercle*).
Une équation polaire reviens en rélaité a ce que tout point de la spirale soit soumis à cette fonction dans laquelle:
- r est la distance entre un point et le centre de la figure,
- θ l'angle entre l'axe des abscisses et le segment R ayant pour extrémité ce point et le centre de la figure.
Par exemple la spirale ci-contre est d'équation r=1.19^θ. Avec a=1 et b=1.19.
*En effet si b=1 alors r=a*1 <=> r=a ce qui est l'équation polaire d'un cercle.


Elle est d'abord étudiée par Descartes et Toricelli mais c'est Varignon qui la nommera spirale logarithmique en premier. Jacques Bernoulli a quant à lui fait graver la spirale sur sa tombre accompagnée de trois mots : « eadem mutata resurgo » / déplacée je réapparaît à l'identique qui désigne son invariance. Hélàs le sculpteur a en réalité dessiné une spirale d’Archimède (d'équation polaire r=aθ) qui ne respecte pas du tout cette caractéristique.



