transition d'échelles. | natureetgeometrie

Relations Inter-échelles

Lorsque l'on parle de géométrie naturelle, nombreuses sont les personnes qui penseront directement aux cristaux, ce qui est compréhensible puisqu'ils sont l'exemple parfait de géométrie à travers les échelles.

Les cristaux sont des éléments naturels qui détiennent un comportement singulier en ce qui concerne leur forme. Cela est nottament provoqué par l'apparition d' une structure singulière au niveau microscopique

Réseau héxagonal

Macroscopique :

Or de telles structures périodiques sont présentes partout autour de nous dans la nature. Par exemple, dans les cristaux de neige, les atomes sont organisés sur un réseau hexagonal ce qui donne de belles figures à six branches.

En 1999, un chercheur américain, Thomas Hales, a réussi à démontrer un théorème qui nous renseigne mieux sur le réseau hexagonal sur une surface plane. Quels sont les pavages du plan avec une tuile d’aire donnée et qui est de périmètre minimal ? Le théorème de Hales stipule que le réseau hexagonal est le plus approprié.

C'est donc une des raisons que l'on retrouve ce réseau héxagonal dans de nombreuses formes de la nature (exemple : Ruche d'abeilles, cristaux de glace ...). En revanche, ce réseau est observé aussi à l'échelle microscopique...

La molécule d'eau (H2O) peut faire 4 liens tétrahédraux d'approximativement 109.5 degrés entre eux: 2 liens covalents (O-H) avec les atomes d'hydrogène de la molécule et 2 ponts hydrogène (O___H) avec les atomes d'hydrogène de molécules voisines. La structure stable de la glace est hexagonale et est nommée Ih. Bien que les atomes d'oxygène de la molécule d'eau aient un emplacement régulier dans la structure hexagonale, les atomes d'hydrogène eux sont placés de façon aléatoire.

Chaque atome d'oxygène possède 2 hydrogènes formant ainsi une molécule d'eau.
Chaque molécule d'eau est orienté de façon à ce que ces hydrogènes soient dirigées vers 2 des 4 atomes d'oxygène qui l'entourent.
L'orientation des molécules d'eau adjacentes se font de façon à ce qu'il n'y ait qu'un seul hydrogène entre 2 oxygènes.
Sous les conditions ordinaires, la glace Ih peut exister dans n'importe quelles des configurations possibles selon la distribution des atomes d'hydrogène dans le cristal.

Microscopique :

Structures Cristallines

Macroscopique :

Un objet est dit posséder une symétrie d'ordre n d'axe (d) lorsqu'il est globalement invariant par une rotation d'angle 2π/n autour de (d). Le cube possède :

Ci-dessous à gauche : 6 axes de symétrie d'ordre 2 (dits axes binaires) passant par les milieux de deux arêtes opposés : (rotations d'angle π) :
Ci-dessous au milieu : 4 axes de symétrie d'ordre 3 (dits axes ternaires) passant par deux sommets opposés (rotations d'angle 2π/3)
Ci-dessous à droite : 3 axes de symétrie d'ordre 4 (dits axes quaternaires) passant par les centres (intersections des diagonales) de deux faces opposées (rotations d'angle 2π/4 = π/2) :

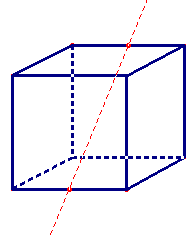
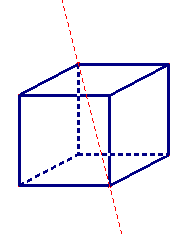
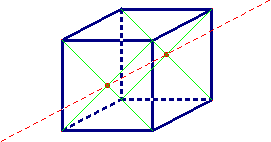
1. Le groupe binaire génère 6 rotations laissant le cube globalement invariant.
2. Le groupe ternaire en génère 8 (d'angles 2π/3 et 2π/3 + 2π/3 ≡ - 2π/3 pour chaque axe)
3 . Le groupe quaternaire 9 (d'angles π/2, 2π/2 = π et 3π/2 ≡ - π/2 pourchaque axe).

Finalement, en ajoutant l'application identique, cela nous conduit à 24 rotations laissant le cube globalement invariant.

(Le cube admet 48 isométries le laissant globalement invariant).

En sachant que certains cristaux ont justement un système cubique (forme de cube)telle que la galène (sulfure de plomb), toute cette symétrie applicable sur les formes géométriques régulières montre que les cristaux ont des propriétés géométriques étonnantes. D'ailleur leur système n'est pas forcement cubique. Le quartz(silice) possède un système rhomboédrique tandis que l' aragonite(variété de carbonate de calcium) possède un système déjà abordé précédemment, le système héxagonal. Mais toutes ses figures singulières sont engendrées par un comportement singulier à l'échelle microscopique...

Microscopique :

Une molécule est un des ensembles de matière les plus petits connus à ce jour, (même si cette affirmation devient de moins en moins juste au fil des découvertes scientifiques), et cet ensemble est constitué d'atomes, composés d'un noyaux qui adoptent une structure plus ou moins remarquable.

La géométrie d'une molécule dépend du nombre d'atome(s) ou de "doublet non liant" reliés à l'atome central de la molécule. Les atomes périphériques subissant une répulsion électronique due à l'interaction faible, qui les force à se repousser les uns les autres, vont se positionner le plus loin possible les uns des autres. Il y a 5 géométries, selon le nombre de "composant" (atome(s) et doublets non liants) de la molécule qui sont liés à l'atome central :

1 composant: positionnement non déterminée car pas de répulsion entre les atomes périphériques.

2 composants: positionnement linéaire selon un angle de 180° entre les atomes périphériques si la molécule est apolaire ou en coude selon un angle de 120° entre les atomes périphérique si la 3molécule est polarisée.

3 composants: positionnement linéaire selon un angle de 120° entre les atomes périphériques.

4 composants: positionnement pyramidal selon un angle de 109° entre les atomes périphériques. Positionnement dit en Tétraèdre.

5 composants: positionnement en diamant (double pyramidal à base triangulaire) selon un angle de 120° équatorialement et 90° axialement, entre les atomes périphériques.

6 composants: positionnement en Octaèdre selon un angle de 90° entre les atomes périphériques.

Il existe aussi des assemblages d'atomes très singuliers, par exemple, la composition d'un solide cristallin qui est constituée par la répétition périodique dans les 3 dimensions de l'espace d'un motif atomique ou moléculaire, appelé maille ; de la même façon qu'un papier peint est constitué de la répétition d'un même motif. La périodicité de la structure d'un cristal est donc représentée par un ensemble de points régulièrement disposés. Cet ensemble est appelé réseau cristallin et les points le constituant sont appelés nœuds du réseau.

À cause de la périodicité du réseau, toute paire de nœuds (O, M) définit un vecteur :

m1,m2 ,m3 étant des entiers relatifs.

Les trois vecteurs a1, a2 et a3 sont linéairement indépendants et constituent une base du réseau cristallin. Pour chaque réseau, il existe une infinité de bases.Une maille élémentaire (ou primitive) est une maille de volume minimal qui contient un seul nœud du réseau. La répétition périodique de cette maille dans les trois dimensions de l'espace suffit à reproduire l'intégralité du réseau et de la structure.

Il existe actuellement 14 réseaux ayant une structure/maille différente...

Pour résumer, les comportements singuliers à notre échelle sont en général engendrés par un autre comportement singulier à une échelle plus petite. La géométrie est donc littéralement présente à touts les niveaux et les met en relations les uns avec les autres. Mais quand est il des entités plus grandes que nous ? ....

Mégascopique